กฎหมายของ Zipf & ลำไส้ใหญ่; มันเชื่อมโยงการเล่นเกมกับทุกสิ่งและทุกอย่างกับการเล่นเกม

เนื้อหา

• กฎหมายของ Zipf อธิบาย
• การทดลองขั้นพื้นฐาน
• กฎหมายของ Zipf ในตลาด Steam
• เราเรียนรู้อะไรเกี่ยวกับ Steam บ้าง
• สรุปผลการวิจัย

เมื่อไม่นานมานี้เพื่อนของฉันคนหนึ่งแนะนำให้ฉันดูวิดีโอของ Vsauces เกี่ยวกับกฎหมายของ Zipf หลักการของ Pareto และการปรากฏตัวที่ลึกลับของพวกเขารอบตัวเรา นี่คือทีเซอร์เล็ก ๆ น้อย ๆ ที่จะได้รับความสนใจของคุณ - 80% ของคนทั้งหมดอาศัยอยู่ใน 20% ของเมืองที่ได้รับความนิยมมากที่สุด 80% ของที่ดินทั้งหมดเป็น 20% ของเจ้าของที่ร่ำรวยที่สุด 80% ของถังขยะทั้งหมดอยู่บนถนนที่มีการทิ้งขยะ 20% สูงสุด - ตามที่กฎหมายของ Zipf และหลักการ Paretos คาดการณ์ไว้

ไม่พอ? เมื่อฉันค้นพบเมื่อวานนี้หลุมกระต่ายไม่หยุดอยู่ที่นั่น ... เต็มไปด้วยความสงสัยฉันตัดสินใจที่จะดูว่าผู้คนใช้เวลาเล่นเกม Steam มากแค่ไหน ... 80% ของผู้คนใช้เวลาเล่นเกมยอดนิยม 20% ... น่าสนใจ? อ่านต่อไปมีเรื่องราวให้มากกว่านี้

การตอกย้ำในเวลา 20 นาทีความพยายามของ Vsauces นั้นยอดเยี่ยมมากและอธิบายภาพขนาดใหญ่จำนวนมากเกี่ยวกับ Zipf แต่เขาเขินอายมากที่แสดงให้เราเห็นถึงกลไกหลักที่เชื่อกันอย่างกว้างขวางว่ามีส่วนสนับสนุนว่าทำไม Zipf ทำงานอย่างไร ดังนั้นก่อนที่เราจะไปผมอยากจะอธิบายสั้น ๆ ว่า

กฎหมายของ Zipf อธิบาย

มีวิธีคิดหลายวิธีในการอธิบายสัญชาตญาณที่อยู่เบื้องหลังหลักการ 20/80 ตัวอย่างที่ดีที่สุดในความคิดของฉันเป็นหนึ่งในหลุมอุกกาบาตดวงจันทร์

การทดลองขั้นพื้นฐาน

ลองจินตนาการดูว่าคุณจะมีดวงจันทร์ที่ไม่มีใครแตะต้อง - เป็นพื้นผิวที่เรียบอย่างสมบูรณ์แบบ ตอนนี้บอกว่ามีดาวเคราะห์น้อยขนาดสุ่มที่เข้าสู่ดวงจันทร์จำใจ เมื่อดินแดนดาวเคราะห์น้อยแรกมันออกจากปากปล่องภูเขาไฟ ตอนนี้อีกหนึ่งความนิยมออกจากปล่องภูเขาไฟที่อื่น แต่ละหลุมอุกกาบาตเป็นส่วนหนึ่งของพื้นที่ผิวทั้งหมดดังนั้นจึงมีโอกาสที่ดาวเคราะห์น้อยดวงถัดไปจะเข้าใกล้กับใบหน้าที่มีอยู่และเข้าร่วมกับมันก่อตัวเป็นกลุ่ม โอกาสที่ดาวเคราะห์น้อยใหม่จะชนกับหลุมอุกกาบาตที่ได้รับนั้นจะเป็นสัดส่วนกับหลุมอุกกาบาตและดาวเคราะห์น้อยขนาดที่มีอยู่ ซึ่งหมายความว่าดาวเคราะห์น้อยแบบสุ่มถัดไปมีแนวโน้มที่จะเข้าร่วมกลุ่มที่ใหญ่ที่สุดที่มีอยู่ทำให้มีขนาดใหญ่ขึ้น กระบวนการสะสมแบบหนึ่งซึ่งจะสร้างกลไกรวย - รวย - รวย - เหงา - รวยขึ้น
โปรดจำไว้เพราะเชื่อกันว่าเป็นคำอธิบายทั่วไปสำหรับ "ทำไม" กฎหมาย Zipfs ทำงานร่วมกับความเป็นสากลที่ลึกลับ ตัวอย่างดาวเคราะห์น้อยนั้นค่อนข้างง่าย แต่คำถามคือสิ่งที่จะเกิดขึ้นในการทำซ้ำหลาย ๆ ครั้ง

สับสนเล็กน้อย?

ฉันทำ gif เพื่อขับจุดแรกนี้ NB! กราฟจะมีการหารือในภายหลังเพียงลองและภาพการทดสอบ

ถ้าเราสังเกตดวงจันทร์จริงปรากฎว่าเมื่อปริมาณของดาวเคราะห์น้อยเพิ่มขึ้นเป็นจำนวนมากขนาดเส้นผ่าศูนย์กลางของปล่องภูเขาไฟที่สังเกตเห็นก็จะเพิ่มขึ้นจนหลุมอุกกาบาตที่ใหญ่ที่สุด 20% เข้ามาใกล้ 80% ของพื้นที่ผิวทั้งหมด

ดังนั้นเมื่อเราไปที่ดาวเคราะห์น้อยมากขึ้นการกระจายตัวของกลุ่มที่ได้รับความนิยมสูงสุดไปจนถึงกลุ่มที่ได้รับความนิยมน้อยที่สุดก็เข้าใกล้ "การกระจายตัวในอุดมคติ" บางอย่างด้วยคุณสมบัติ 20/80 - การกระจายพาเรโต ถ้าคุณทำคณิตศาสตร์มันกลับกลายเป็นว่า (โดยทั่วไป) หากกลุ่มที่ใหญ่ที่สุดมีขนาด N กลุ่มที่ใหญ่เป็นอันดับสองจะมีขนาดประมาณ N / 2, N / 3 ที่สามเป็นต้นไปเรื่อย ๆ สิ่งนี้เรียกว่ากฎของ Zipf สิ่งที่แปลกก็คือกฎของ Zipf และการแจกจ่าย Pareto ทำงานเพื่อองค์ประกอบที่น่าพิศวง (ดาวเคราะห์น้อย) และกลุ่ม (กลุ่มปล่องภูเขาไฟ) แน่นอนว่ามีการบิดเบือนและการสุ่ม แต่มีแนวโน้มทั่วไปที่ปฏิเสธไม่ได้
ฉันหวังว่าคุณจะเห็นว่าดาวเคราะห์น้อยมีแนวโน้มที่จะกระทบกับหลุมอุกกาบาตขนาดใหญ่บนดวงจันทร์ได้อย่างไรเชื่อมต่อกับเมืองที่น่าสนใจยิ่งขึ้นหากมีผู้คนอาศัยอยู่ในพวกเขามากขึ้น อย่างไรก็ตามสิ่งหนึ่งที่ต้องตระหนักคือเมืองอยู่ห่างไกลจาก "กลุ่ม" เพียงกลุ่มเดียวที่มีพฤติกรรมตาม Zipf

นี่คือตัวอย่างจากการวิจัยของ Mark Newmans เกี่ยวกับการแจกแจงพาเรโต NB! กราฟอยู่ในระดับล็อก - ล็อกซึ่งทำให้ไฮเพอร์โบลิกของเส้นโค้งราบเรียบซึ่งนำเสนอความสัมพันธ์เชิงเส้นเกือบ

เริ่มต้น y = aX ^ (- b)
บันทึกของทั้งสองฝ่าย => log y = log a - b log X

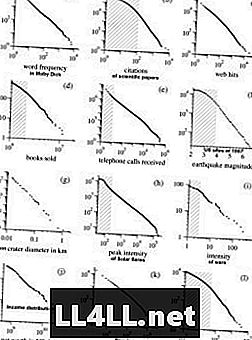
ที่น่าสนใจก็คือแนวโน้มเดียวกันนี้แสดงโดยลัทธิทางศาสนา ... ทรัพย์สินที่ใช้ร่วมกันของปรากฏการณ์เหล่านี้ส่วนใหญ่เป็นเพียงแนวโน้ม "กลุ่มใหญ่ - ใหญ่ - ใหญ่" ดังนั้นกฎของ Zipf จึงยังคงอยู่ในกลไกซึ่งการกำหนดลักษณะขององค์ประกอบนั้นเชื่อมโยงกับขนาดกลุ่ม (ความหมายยิ่งกลุ่มยิ่งมีโอกาสมากขึ้นก็จะยิ่งเติบโตมากขึ้น) นี่คือเหตุผลที่ฉันชอบคิดว่ากลุ่มเป็นกลุ่มและองค์ประกอบเป็นคลัสเตอร์

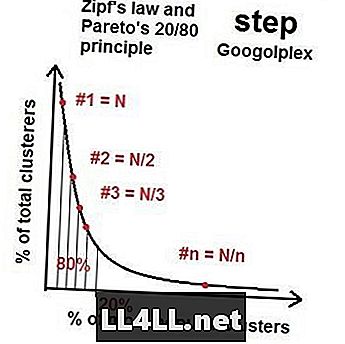
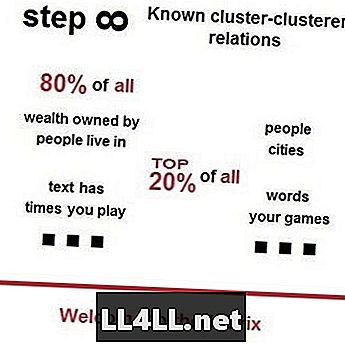
กฎหมายของ Zipf ในตลาด Steam

สงสัยว่าอันสุดท้ายหรือไม่ นี่คือเวลาที่ผู้คนใช้ในเกมยอดนิยมบน Steam .. ข้อมูลจาก SteamSpy

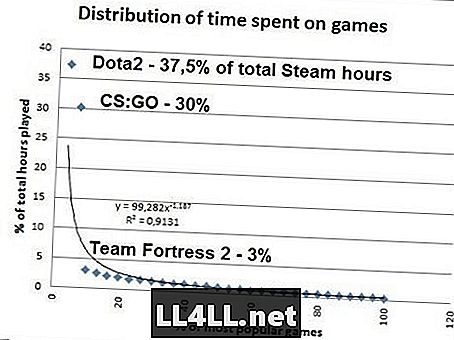
ถ้าคุณทำคณิตศาสตร์มันกลับกลายเป็นว่า 20% ของเกม Steam ที่ได้รับความนิยมมากที่สุดคิดเป็น 80% ของจำนวนทั้งหมดของการเล่นดังนั้น Pareto 20/80 ลึกลับทำงานเหมือนมีมนต์เสน่ห์ที่นี่ ... สิ่งหนึ่งที่ต้องสังเกตคือ Zipf เป็นจริง CS: GO ต้องการบัญชี 37,5% / 2 = 18,8% ของเวลาทั้งหมดแทนที่จะเป็น 30% แต่นอกเหนือจากค่าเริ่มต้นนี้ (หยุดเล่น CS: GO) การกระจายแบบ Zipf นั้นชัดเจน

นี่คือจำนวนสำเนาที่ขายสำหรับเกมที่ได้รับความนิยมสูงสุด

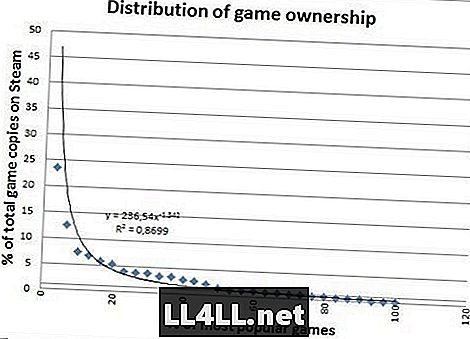
ดูดีกว่าใช่มั้ย สำเนาที่ขายไม่ได้มีค่าผิดปกติจำนวนมากดังนั้นจึงเหมาะสมเป็นอย่างดีซึ่งเป็นข้อแตกต่างที่น่าสังเกต อย่างไรก็ตามมีสิ่งที่น่าสนใจมากกว่าที่จะสรุปจากความแตกต่างของกราฟสองกราฟล่าสุด
คุณสังเกตหรือไม่ว่า "หาง" ไปทางขวาเป็นไขมันชนิดใดในกราฟที่สอง? ในแง่ง่าย ๆ สิ่งนี้บอกเราว่าเกม "ค่อนข้างไม่เป็นที่นิยม" นั้นเป็นเกมที่ได้รับความนิยมมากกว่าเกมที่แล้ว
ในความเป็นจริงปรากฎว่าเกมยอดนิยม 20% คิดเป็นเพียง 60% ของยอดขายเทียบกับ 80% ของการเล่น ที่น่าสนใจ? คุณเดิมพันตูดของคุณมันเป็น

เราเรียนรู้อะไรเกี่ยวกับ Steam บ้าง

ความจริงที่ว่าความนิยมของเกมดังต่อไปนี้การกระจายของ Pareto บอกเราว่าจริง ๆ แล้วมีเอฟเฟกต์เครือข่ายที่เป็นบวกบางประเภทซึ่งทำให้ผู้เล่นเลือกเกมที่มีผู้เล่นจำนวนมากแล้ว ความแตกต่างของความอ้วนของก้อยนั้นบอกเราว่าผู้ใช้ Steam มี "กลุ่มคนตาบอด" มากขึ้นเมื่อซื้อเกมมากกว่าตอนที่พวกเขาเล่น
ลองคิดดู - ผู้คนจำนวนมากซื้อเกมโดยไม่คำนึงถึง "ความนิยมในปัจจุบัน" ยิ่งมีการแจกแจงพาเรโตมากขึ้นเท่าไหร่มันก็มีโอกาสน้อยที่เกมใหญ่จะเติบโตต่อไป หากไม่มีใครบอกว่ามีคนเล่นเกมแล้วเท่าไรและความพร้อมใช้งานของเกมทั้งหมดเท่ากันเราก็คาดหวังว่าเกมยอดนิยม 20% จะคิดเป็น 50% ของยอดขายและเวลาเล่น กระจายตามปกติ)

สรุปผลการวิจัย

ดังนั้นจึงมีสองปัจจัยที่มีส่วนช่วยในการกระจาย Pareto ในตลาด Steam - วิธีการที่นักพัฒนานวัตกรรม (จำนวนหลุมอุกกาบาตดวงใหม่จะเกิดขึ้น) และจำนวนนักเล่นเกม (ดาวเคราะห์น้อย) ให้ความสำคัญกับขนาดกลุ่มปัจจุบันเมื่อเลือกกลุ่มที่จะเข้าร่วม . ตามที่ปรากฎออกมานักเล่นเกมมีขนาดกลุ่มคนตาบอดมากเมื่อซื้อเกม แต่กลับตรงกันข้ามเมื่อพวกเขาเล่นเกม เจ๋งเหรอ?

หากคุณต้องการเรียนรู้เพิ่มเติมเกี่ยวกับกฎของ Zipf และการแจกแจงกฎกำลังนี่คือการบรรยายที่ดี นอกจากนี้อย่าลืมมองกระดาษของนิวแมนด้วย!
หากคุณต้องการอ่านเนื้อหาประเภทนี้มากขึ้นในไม่ช้าฉันจะพยายามเข้าร่วมการสังเกตการณ์กับโมเดลซึ่งแสดงให้เห็นว่าเกมที่มีผู้เล่นหลายคนที่เป็นที่นิยมมากขึ้นมีราคาสูงกว่า (ซึ่งเชื่อมโยงกับความต้องการของนักเล่นเกม ดูบทความที่นี่ บทความการต่อต้านอย่างต่อเนื่องของชิ้นส่วนจะพยายามและเข้าร่วมทฤษฎีเหล่านี้ร่วมกันอธิบายว่าเกมที่มีผู้เล่นหลายคนเครือข่ายสังคมและเมืองเป็นอย่างไรในความเป็นจริงสินค้าต่อต้านคู่แข่งที่มีเอฟเฟกต์เครือข่าย (ยิ่งมีคนบริโภคมากขึ้น ให้สิทธิ์พวกเขาด้วยหมอกแห่งความลึกลับของ Zipfian ...

จนกว่าจะถึงตอนนั้นจงสนุกกับตัวคุณเอง!

ป.ล. แสดงความคิดเห็นด้วยไอเดียสนุก ๆ สำหรับความสัมพันธ์ 20/80 ที่คุณคิดว่าอาจเป็นเรื่องจริง

ของฉันคือ:
80% ของความคิดถึงคนเกิดจาก 20% ของความทรงจำที่มีความสุขที่สุดของพวกเขา (พิสูจน์ได้จริงสำหรับคนที่ลืมอัตราข้อมูลที่)
80% ของมวลรวมอยู่ใน 20% ของวัตถุอวกาศที่ใหญ่ที่สุด (พิสูจน์แล้วจริง ๆ ว่ามีการกระจายแรงโน้มถ่วง)
และแน่นอน
ความยุ่งเหยิง 80% ในห้องน้ำของคุณมาจาก 20% ของสิ่งที่คุณกิน (ไม่มีงานวิจัยทางวิชาการที่จะพูดถึง)